Dear all, I dont know if here is the rigth place to post this, but as I need quick help I think that here is a good better place than in github isses.
I need to implement FSi coupling preCICE+OpenFOAM+FenicsX, but as I understand the fenicsx adapter have all the limitantions that I need ![]()
1- don’t support FSI at the moment
2- is only for 2D
3- is not ported yet for preCICEv3
So I decideto doit by myself based on the current fenicsx adapter but with a lot of simplifications. Here is my code at the moment:
import precice
import os
import json
import sys
import numpy as np
import dolfinx as dfx
from petsc4py import PETSc
import logging
logger = logging.getLogger("precice")
class Config:
"""
Handles reading of config. parameters of the fenicsxadapter based on JSON
configuration file. Initializer calls read_json() method. Instance attributes
can be accessed by provided getter functions.
"""
def __init__(self, config_path: str):
self._config_file = config_path
self._precice_config = None
self._participant = None
self._mesh = None
self._read_data = None
self._write_data = None
self._patch_tags = []
self.read_json(config_path)
def read_json(self, config_path: str):
"""
Reads JSON adapter configuration file and saves the data to the respective instance attributes.
Parameters
----------
config_path : string
Name of the JSON configuration file
"""
read_file = open(config_path, "r")
data = json.load(read_file)
folder = os.path.dirname(
os.path.join(os.getcwd(), os.path.dirname(sys.argv[0]), config_path)
)
self._precice_config = os.path.join(folder, data["precice_config"])
self._participant = data["participant"]
self._mesh = data["interface"]["mesh"]
try:
self._write_data = data["interface"]["write_data"]
except KeyError:
# not required for one-way coupling, if this participant reads data
self._write_data = None
try:
self._read_data = data["interface"]["read_data"]
except KeyError:
# not required for one-way coupling, if this participant writes data
self._read_data = None
read_file.close()
@property
def precice_config(self):
return self._precice_config
@property
def participant(self):
return self._participant
@property
def mesh(self):
return self._mesh
@property
def patch_tags(self):
return self._patch_tags
@property
def read_data(self):
return self._read_data
@property
def write_data(self):
return self._write_data
class FunctionData:
def __init__(self, vector_space, interface_dof):
self.V = vector_space
self._dim = self.V.mesh.geometry.dim
self._v_space_coords = self.V.tabulate_dof_coordinates()[:, : self._dim]
self._interface_dof = interface_dof
self._vector_size = len(self._v_space_coords.flatten())
self._vector = PETSc.Vec().createMPI(self._vector_size, comm=PETSc.COMM_WORLD)
self._vector.setFromOptions()
self._vector.setUp()
self.reset()
def reset(self):
self._vector.set(0.0)
self._vector.assemble()
def setValues(self, values):
self.reset()
arr = self.vector.getArray()
arr = arr.reshape(-1, self._dim)
arr[self._interface_dof] = values
start, end = self._vector.getOwnershipRange()
self._vector[start:end] = arr[start:end]
self._vector.assemble()
def __str__(self):
if self._dim == 3:
Fx, Fy, Fz = self.array.sum(axis=0)
return f"Sum Fx: {Fx:.2f}, Sum Fy: {Fy:.2f}, Sum Fz:{Fz:.2f}"
if self._dim == 2:
Fx, Fy = self.array.sum(axis=0)
return f"Sum Fx: {Fx:.2f}, Sum Fy: {Fy:.2f}"
@property
def array(self):
return self._vector.getArray().reshape(-1, self._dim)
@property
def coords(self):
fs_coords = self.V.tabulate_dof_coordinates()
return fs_coords[self._interface_dof]
@property
def vector(self):
return self._vector
class SolverState:
def __init__(self, u, v, a, t, n):
self.u = u
self.v = v
self.a = a
self.t = t
self.n = n
def get_state(self):
return self.u, self.v, self.a, self.t, self.n
def __str__(self):
u, v, a, t, n = self.get_state()
return f"u={u}, v={u}, a={u}, t={t}, n={n}"
class Adapter:
def __init__(self, mpi_comm, config_path: str, mesh) -> None:
self._config = Config(config_path)
self._comm = mpi_comm
self._domain = mesh
self._topology = self._domain.topology
self._checkpoint = None
self._interface_nodes_coords = None
self._function_space = None
self._interface = precice.Participant(
self._config.participant,
self._config.precice_config,
self._comm.Get_rank(),
self._comm.Get_size(),
)
self._dim = self._interface.get_mesh_dimensions(self._config.mesh)
self._fdim = self._domain.geometry.dim - 1
assert (
self._dim == self._domain.geometry.dim
), "Mesh in the config file and the mesh provided have different dimensions"
def interpolation_points_in_vector_space(self):
V = self._function_space
fs_coords = V.tabulate_dof_coordinates()
fs_coords = fs_coords[:, : self._dim]
boundary_dofs = dfx.fem.locate_dofs_topological(V, self._fdim, self._facesets)
boundary_coords = fs_coords[boundary_dofs]
return boundary_dofs, boundary_coords
def initialize(self, function_space, facesets):
self._function_space = function_space
self._facesets = facesets
self._facesets_tags = dfx.mesh.meshtags(self._domain, self._fdim, np.sort(facesets), 1)
self._interface_dof, self._interface_dof_coords = (
self.interpolation_points_in_vector_space()
)
self._precice_vertex_ids = self._interface.set_mesh_vertices(
self._config.mesh, self._interface_dof_coords
)
self._function_data = FunctionData(self._function_space, self._interface_dof)
if self._interface.requires_initial_data():
self._interface.write_data(
self._config.mesh,
self._config.write_data,
self._precice_vertex_ids,
np.zeros(self._interface_dof_coords.shape),
)
self._interface.initialize()
return self._function_data
@property
def interface_ids(self):
return self._interface_dof
@property
def interface_coordinates(self):
return self._interface_dof_coords
@property
def precice(self):
return self._interface
@property
def dt(self):
return self._interface.get_max_time_step_size()
def is_coupling_ongoing(self):
return self._interface.is_coupling_ongoing()
def is_time_window_complete(self):
return self._interface.is_time_window_complete()
def requires_reading_checkpoint(self):
return self._interface.requires_reading_checkpoint()
def requires_writing_checkpoint(self):
return self._interface.requires_writing_checkpoint()
def advance(self, dt: float):
return self._interface.advance(dt)
def finalize(self):
return self._interface.finalize()
def read_data(self, dt):
mesh_name = self._config.mesh
data_name = self._config.read_data
read_data = self._interface.read_data(mesh_name, data_name, self._precice_vertex_ids, dt)
return read_data
def write_data(self, write_function):
mesh_name = self._config.mesh
write_data_name = self._config.write_data
write_data = write_function.x.array.reshape(-1, self._dim)[self.interface_ids]
self._interface.write_data(mesh_name, write_data_name, self._precice_vertex_ids, write_data)
def store_checkpoint(self, u, v, a, t, n):
self._checkpoint = SolverState(u.copy(), v.copy(), a.copy(), t, n)
def retrieve_checkpoint(self):
assert not self.is_time_window_complete()
return self._checkpoint.get_state()
And flap tutorial code will looks like this:
import numpy as np
import ufl
import os
from mpi4py import MPI
import dolfinx as dfx
import dolfinx.fem.petsc
from dolfinx.mesh import create_rectangle, CellType
from petsc4py import PETSc
from dolfinx.fem.petsc import LinearProblem
# --------- #
# CONSTANTS #
# --------- #
MPI_COMM = MPI.COMM_WORLD
CURRENT_FOLDER = os.path.dirname(__file__)
PARTICIPANT_CONFIG = os.path.join(CURRENT_FOLDER, "precice-config.json")
RESULTS_DIR = os.path.join(CURRENT_FOLDER, "results")
os.makedirs(RESULTS_DIR, exist_ok=True)
os.chdir(CURRENT_FOLDER)
WRITER = dfx.io.VTKFile(MPI_COMM, f"{RESULTS_DIR}/result.pvd", "w")
WIDTH, HEIGHT = 0.1, 1
NX, NY = 4, 26
E = 4000000.0
NU = 0.3
RHO = 3000.0
BETA_ = 0.25
GAMMA_ = 0.5
# ------- #
# MESHING #
# ------- #
domain = create_rectangle(
MPI_COMM,
[np.array([-WIDTH/2, 0]), np.array([WIDTH/2, HEIGHT])],
[NX, NY],
cell_type=CellType.quadrilateral,
)
dim = domain.topology.dim
WRITER.write_mesh(domain)
# -------------- #
# Function Space #
# -------------- #
degree = 2
shape = (dim,) # this means we want a vector field of size `dim`
V = dfx.fem.functionspace(domain, ("P", degree, shape))
u = dfx.fem.Function(V, name="Displacement")
f = dfx.fem.Function(V, name="Force")
# ------------------- #
# Boundary conditions #
# ------------------- #
tol = 1e-14
def clamped_boundary(x):
return abs(x[1]) < tol
def neumann_boundary(x):
"""
determines whether a node is on the coupling boundary
"""
return np.logical_or((np.abs(x[1] - HEIGHT) < tol) , np.abs(np.abs(x[0]) - WIDTH / 2) < tol)
fixed_boundary = dfx.fem.locate_dofs_geometrical(V, clamped_boundary)
coupling_boundary = dfx.mesh.locate_entities_boundary(domain, dim - 1, neumann_boundary)
coupling_boundary_tags = dfx.mesh.meshtags(domain, dim-1, np.sort(coupling_boundary), 1)
bcs = [dfx.fem.dirichletbc(np.zeros((dim,)), fixed_boundary, V)]
# ------------ #
# PRECICE INIT #
# ------------ #
participant = Adapter(MPI_COMM, PARTICIPANT_CONFIG, domain)
_f = participant.initialize(V, coupling_boundary)
with open(f"{RESULTS_DIR}/interpolation_points.csv", "w") as p_file:
p_file.write("X,Y,Z\n")
np.savetxt(p_file, _f.coords, delimiter=",")
dt = dfx.fem.Constant(domain, PETSc.ScalarType(participant.dt))
# ------------------------ #
# linear elastic equations #
# ------------------------ #
E = dfx.fem.Constant(domain, E)
nu = dfx.fem.Constant(domain, NU)
rho = dfx.fem.Constant(domain, RHO)
lmbda = E * nu / (1 + nu) / (1 - 2 * nu)
mu = E / 2 / (1 + nu)
def epsilon(v):
return ufl.sym(ufl.grad(v))
def sigma(v):
return lmbda * ufl.tr(epsilon(v)) * ufl.Identity(dim) + 2 * mu * epsilon(v)
# ------------------- #
# Time discretization #
# ------------------- #
# prev time step
u_old = dfx.fem.Function(V)
v_old = dfx.fem.Function(V)
a_old = dfx.fem.Function(V)
# current time step
a_new = dfx.fem.Function(V)
v_new = dfx.fem.Function(V)
beta = dfx.fem.Constant(domain, BETA_)
gamma = dfx.fem.Constant(domain, GAMMA_)
dx = ufl.Measure("dx", domain=domain)
ds = ufl.Measure("ds", subdomain_data=coupling_boundary_tags)
a = 1 / beta / dt**2 * (u - u_old - dt * v_old) + a_old * (1 - 1 / 2 / beta)
a_expr = dfx.fem.Expression(a, V.element.interpolation_points())
v = v_old + dt * ((1 - gamma) * a_old + gamma * a)
v_expr = dfx.fem.Expression(v, V.element.interpolation_points())
# ------------------ #
# mass, a stiffness #
# ------------------ #
u_ = ufl.TestFunction(V)
du = ufl.TrialFunction(V)
def mass(u, u_):
return rho * ufl.dot(u, u_) * dx
def stiffness(u, u_):
return ufl.inner(sigma(u), epsilon(u_)) * dx
L = ufl.dot(f, u_) * ds(1) # include wind loads over surface
Residual = mass(a, u_) + stiffness(u, u_) - L
Residual_du = ufl.replace(Residual, {u: du})
a_form = ufl.lhs(Residual_du)
L_form = ufl.rhs(Residual_du)
opts = PETSc.Options() # type: ignore
opts["ksp_type"] = "cg"
opts["ksp_rtol"] = 1.0e-8
opts["pc_type"] = "gamg"
# Use Chebyshev smoothing for multigrid
opts["mg_levels_ksp_type"] = "chebyshev"
opts["mg_levels_pc_type"] = "jacobi"
# Improve estimate of eigenvalues for Chebyshev smoothing
opts["mg_levels_ksp_chebyshev_esteig_steps"] = 10
problem = LinearProblem(a_form, L_form, u=u, bcs=bcs, petsc_options=opts.getAll())
# parameters for Time-Stepping
t = 0.0
n = 0
while participant.is_coupling_ongoing():
if participant.requires_writing_checkpoint(): # write checkpoint
participant.store_checkpoint(u_old, v_old, a_old, t, n)
dt.value = participant.dt
read_data = participant.read_data(dt)
start1, end1 = _f.vector.getOwnershipRange()
start2, end2 = f.vector.getOwnershipRange()
_f.setValues(read_data)
f.vector[start2:end2] = _f.vector[start1: end1]
f.vector.assemble()
problem.solve()
f.x.scatter_forward()
u.x.scatter_forward()
# Write new displacements to preCICE
participant.write_data(u)
# Call to advance coupling, also returns the optimum time step value
participant.advance(float(dt))
# Either revert to old step if timestep has not converged or move to next timestep
if participant.requires_reading_checkpoint():
u_cp, v_cp, a_cp, t_cp, n_cp = participant.retrieve_checkpoint()
u_old.interpolate(u_cp)
v_old.interpolate(v_cp)
a_old.interpolate(a_cp)
t = t_cp
n = n_cp
else:
v_new.interpolate(v_expr)
a_new.interpolate(a_expr)
u.vector.copy(u_old.vector)
v_new.vector.copy(v_old.vector)
a_new.vector.copy(a_old.vector)
t += dt
n += 1
print("===================================================================")
u_values =u.x.array.reshape((-1, dim)).sum(axis=0)
print(_f)
if dim == 3:
print(f"Sum Ux: {u_values[0]:.2e}, Sum Uy: {u_values[1]:.2e},Sum Uz: {u_values[2]:.2e}")
if dim == 2:
print(f"Sum Ux: {u_values[0]:.2e}, Sum Uy: {u_values[1]:.2e}")
print("===================================================================")
if participant.is_time_window_complete():
if n % 10 == 0:
WRITER.write_function(u, t)
WRITER.write_function(f, t)
WRITER.close()
WRITER.close()
participant.finalize()
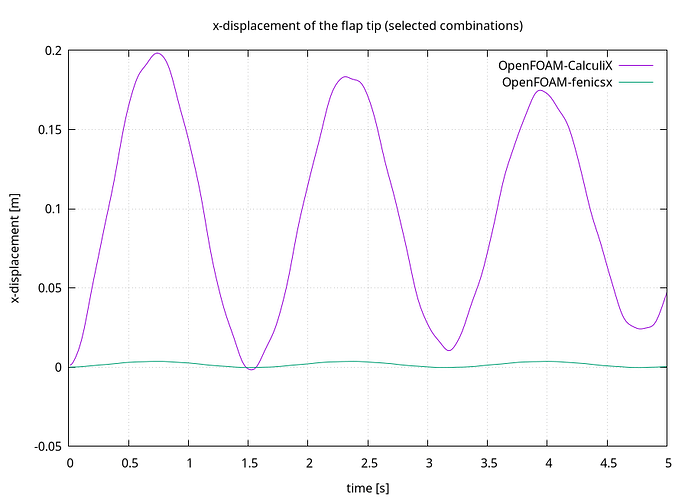
And it runs until the end but the results are very inaccurate, and I can’t figure put where is the mistake.
can someone help me with this?
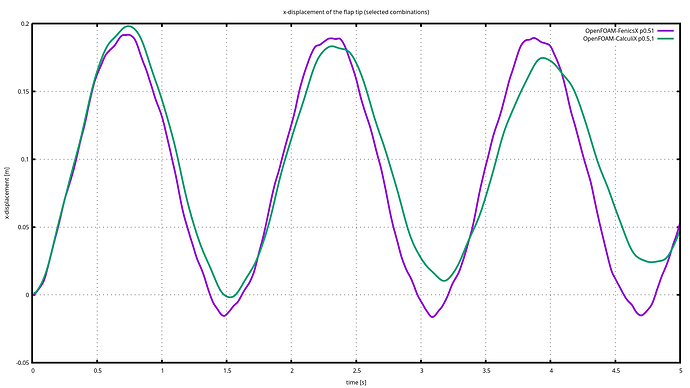
Update
seems that I have an scaling problem here, in this next chart I multiply the Displacement in fenix *100, and seems to be OK. I test with other points and seems to be reproducible.
I hav e a question about wathc point. the data of the wathc point are the received data frome the other participant or are they interpolated on the mesh receptor mesh point. Im, asking this, because If I plot the Forces for calculix and for FenicsX in te same point they are not to far. So my gess is that there is something wrong on my solver or in the way that I map the force to the boundary